About

I am a Ph.D. candidate in Chemical Engineering at Lehigh University, working with Dr. Kothare and Dr. Rangarajan. I completed my Master’s degree at Rutgers University under the guidance of Dr Ierapetritou and my undergraduate studies at the Institute of Chemical Technology (ICT), Mumbai, India.

My research lies at the intersection of dynamic process modeling, optimization and scientific machine learning. In particular,

• Constrained Nonlinear Optimization
• Parameter estimation of ordinary (partial) differential equations
• Physics informed machine learning of ordinary and partial differential equations
• Constrained differential dynamic programming for solving optimal control problems

To support this research, I have also developed open-source software tools to ensure reproducibility and accessibility for the broader research community.

Outside of research, I enjoy reading (including manga), investing, and hiking.

Research Summary

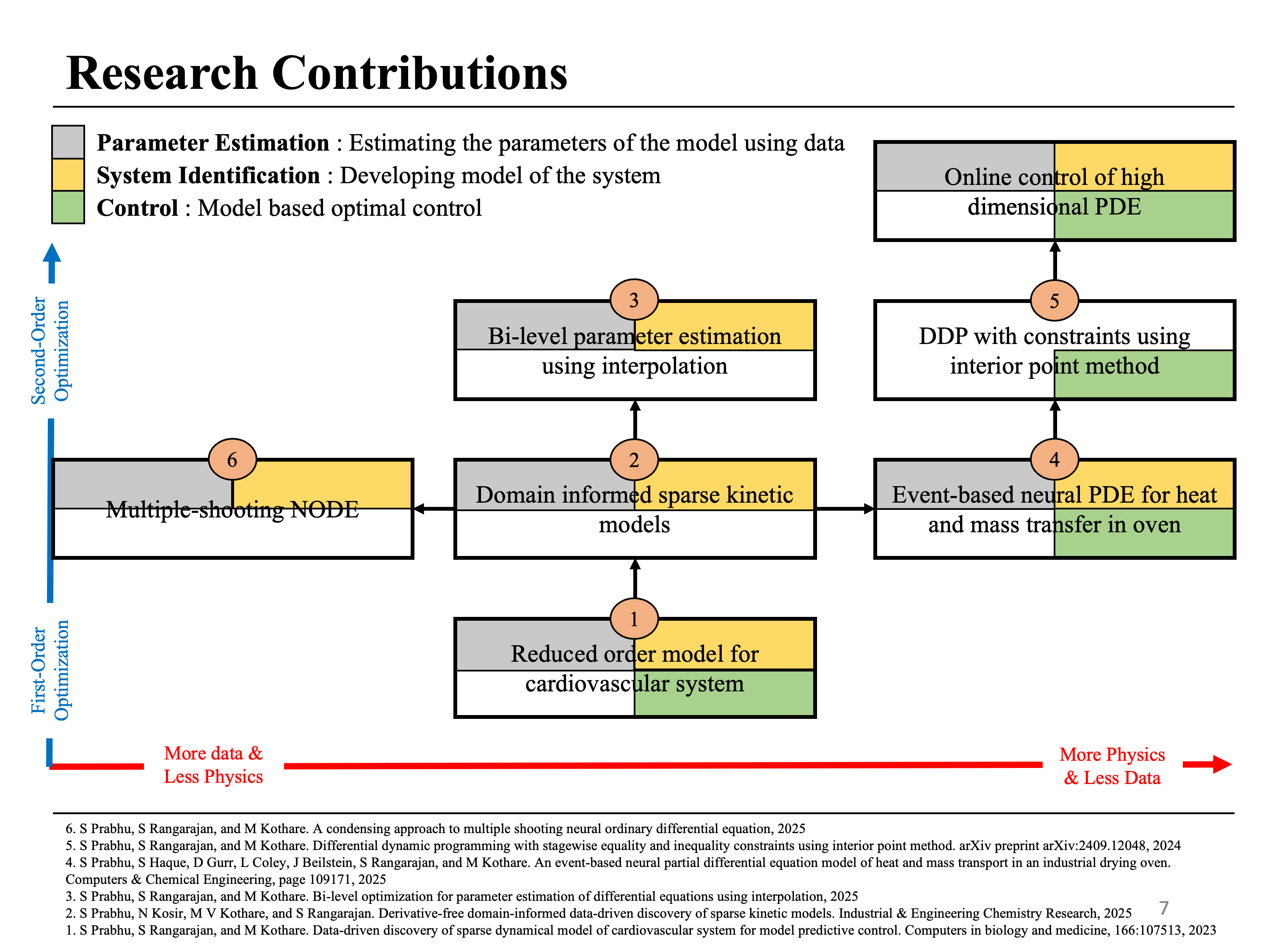
Throughout my PhD, my research has focused on using data to achieve the following objectives:

• Parameter estimation: given a set of (neural) ordinary differential equations (ODEs), we estimate the parameters that best describe the measured data.
• System identificaiton: we discover the underlying ODEs, either through mechanistic modeling or data-driven approaches, and subsequently perform parameter estimation.
• Optimal control: Once the model has been trained and validated, we use the estimated model to design and implement control strategies for the system.

I began my PhD by developing reduced-order dynamic models of the cardiovascular system using patient-specific data (Project 1 in the figure). However, the method we employed, Sparse Identification of Nonlinear Dynamics (SINDy), is highly sensitive to noise, as it required computing derivatives of measurements. To address this challenge, we developed a derivative-free variant, DF-SINDy, which eliminates the need for derivative computations by working with integral terms or directly with the measurements, while maintaining convexity of the problem (Project 2 in the figure). Nonetheless, both of these methods assume that the parameters appear linearly in the dynamic equations. To overcome this limitation, we developed a bilevel optimization framework (Project 3 in the figure) that generalizes DF-SINDy to a broader class of ordinary differential equations, regardless of whether the parameters appear linearly or nonlinearly.

In cases where domain knowledge is limited but abundant data is available, the unknown dynamical equations can be approximated using a neural network. Such models are referred to as neural ordinary differential equations (NODEs). However, NODEs are notoriously difficult to train on highly oscillatory and nonlinear data—conditions that are common in many scientific applications. To address this challenge, we developed a multiple-shooting training procedure (Project 6 in the figure), which partitions the entire trajectory into smaller intervals that can be integrated independently. Continuity across these intervals is then enforced through additional equality constraints.

On the other hand, where domain knowledge is abundant and data is limited, it is still possible to build models by incorporating both sources of information. This approach was implemented in the context of solid drying (Project 4 in the figure) at Owens Corning, where we developed a mechanistic partial differential equation (PDE) model and replaced certain parameters of the mechanistic model with neural networks. This hybrid framework not only introduces flexibility but also captures unmodeled effects. We demonstrated that, even with limited, partially observed, and spatially sparse data, such a model can accurately reproduce the system dynamics and generalize to unseen process conditions. Although training is significantly accelerated through our custom ODE solver implemented in JAX, real-time (online) control remains computationally demanding and currently infeasible. To mitigate this issue, we developed an interior-point-based differential dynamic programming (DDP) algorithm capable of handling general stagewise inequality and equality constraints (Project 5 in the figure). This dynamic programming approach reduces the computational complexity of the optimal control problem from cubic or quadratic to linear with respect to the control horizon. However, the computational cost still remains cubic in the state and control dimensions.

At present, my research focuses on data-driven approaches for high-dimensional PDEs, with an emphasis on enabling efficient online control.